Главная • Грамматика • Упражнения • Карта сайта • Topics • Workbook • Учебники • Тесты • Темы• О любви

Основные арифметические выражения, формулы, уравнения
и правила их чтения на английском языке.

( )	round brackets; parentheses
{ }	curly brackets; braces
[ ]	square brackets; brackets
a = b	a equals b; or a is equal to b
a ≠ b	a is not equal to b
a > b	a is greater than b
a2 > ad	a second is greater than a dth
b < a	b is less than a
a >> b	a is substantially greater than b
a ≥ b	a is greater than or equal to b
	x trends to infinity
	a vector ; the mean volume of a
	the first derivative
	the second derivative
9.510	nine thousand five hundred and ten
32 + 8 = 40	thirty-two plus eight is (are) forty; or, thirty-two plus eight equals forty; or, thirty-two plus eight is equal to forty; or, eight added to thirty-two makes forty
20 - 5 = 15	twenty minus five is fifteen; or, twenty minus five is equal to (equals) fifteen; or, twenty minus five leaves fifteen; or, five from twenty is (leaves) fifteen
	a plus or minus b
1 × 1 = 1	once one is one
2 × 2 = 4	twice two is (equals) four; or, twice two makes four
6 × 10 = 60	six multiplied by ten equals sixty; or, six multiplied by ten is (equal to) sixty; or, six times ten is sixty
work = force × distance	work is (equal' to) the product of the force multiplied by the distance; or, work is (equal to) the product of force times the distance
12 : 3 = 4	twelve divided by three equals (is) four
	a (one) half
	a (one) third
	two-thirds
	five-ninths
4½	four and a half
	eight and three-quarters
0.6 or .6	point six
5.34	five point thirty-four; or, five point three four
2.01	two point nought one; or two point o [ou] one
0.007	point nought nought seven; or, point two oes [ouz] seven
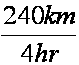	240 kilometers pro 4 hours
8 : 4 = 2	the ratio of eight to four is two.
20 : 5 = 16 : 4 or	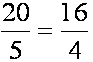the ratio of twenty to five equals (is equal to) the ratio of sixteen to four; or, twenty is to five as sixteen is to four
20°	twenty degrees
6´	six minutes; also, six f eet
10´´	ten seconds; also, ten inches
a´	a prime
a´´	a second prime; or a double prime; or a twice dashed
a´´´	a triple prime
92	nine square, or, the square of nine or, nine to the second power
63	six cubed; or, six to the third (power)
c18	c [si:] to the eighteenth (power)
a-10	a [ei] to the minus tenth (power)
	the square root (out) of four is (equals) two
	the square root of a
	the cube root of a
	the fifth root of a square
	a plus b all squared
	L equals the square root (out) of R square plus x square
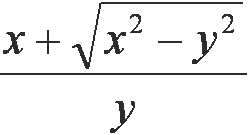	x plus square root of x square minus y square all over y
	the tenth root (out) of a square plus b square
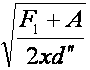	square root out of F first plus A divided by two xd th twice dashed (or double prime)
	a to the m/n th power equals the nth root out of a to the mth (power)
	dz over dx
	y is a function of x
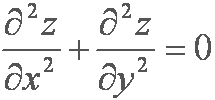	partial d two z over partial dx plus partial d two z over partial dy equals zero
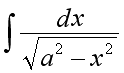	indefinite integral of dx (divided) by the square root out of a2 minus x2
	integral from zero to µ (mu)
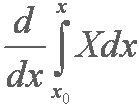	d (divided) by dx (or d over dx) of the integral from x nought to x of X large dx
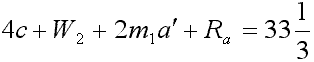	4c plus W second plus 2 m first a prime plus R ath equals thirty-three and one-third
	V equals u square root of sine square i minus cosine square i equals u
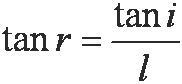	tangent r equals tangent i divided by l
	the logarithm of two equals zero point three o[ou] one
	a is equal to the logarithm of d to the base c
	u is equal to the integral of f sub one of x multiplied by dx plus the integral of f sub two of y multiplied by dy
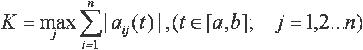	K is equal to the maximum over j of the sum from i equals one to i equals n of the modulus of aij of t , where t lies in the closed interval ab and where j runs from one to n
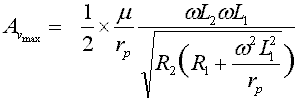	A vmax is equal to one half mu by r pth omega L second omega L first (divided) by square root out of R second round brackets opened R first plus omega square L first square by r pth round brackets closed
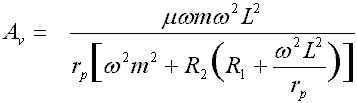	Av is equal to mu omega m omega square L square (divided) by r pth square brackets opened omega square m square plus R second round brackets opened R first plus omega square L square (divided) by r pth round and square brackets closed